XAI demand continues to grow across all industries primarily in finance and medical science. Before we decline loan, increase EMI amount or suggest some medical treatment (as a proactive measure), we need to have all pertinent data, indicators and logic to explain the rationale and situation to the consumers.
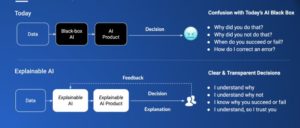
Stakeholders ranging from regulators, governance to the customers challenge AI/ML outcome, they look for FAT (Fair, Accountable, Transparence) models. We just can’t get away by celebrating superb score [e.g. high F1(~1) score in classifier or high R2 in regression or optimal confusion matrix score (high TPR and low FPR etc.)] at the cost of less explainability. Adequate technique and effort must have to be applied to connect business case (problem statement) to the model outcome through internal working of ML models to establish proper transparency, inferabilty & explainability. We usually find difficult to map internals of black box (Trained models built out of ‘ANN’,’CNN’,’RNN’,’LTSM’ and few others along with its mathematical constructs such as auto features constructions, back propagation, nonlinear activation functions, filter size, regularization parameters and several others) to business domain vis-à-vis model behaviors to stakeholders, though model performs really well. Black box could still be operational in sales & marketing area to tap untapped customers (while adhering to regulatory compliances BASEL, GDPR, CCPA, various data privacy acts etc.) but not in core business functions such as mortgage, wealth management, risk, lending, drug synthesis, genomics and many others unless these are explainable and transparent. Model governance works in tune with govt. regulations, model transparency, de-biasing data, business target etc. hence ready to sacrifice performance (accuracy) of models to increase FAT. We are already in XAI phase of AI journey and challenge is to improve models inferabilty & explainability without compromising too much on its performance.
This article is an attempt to unravel the constructs and mechanics of AI/ML model behavior and increase explainability by zooming into feature engineering.
Singular Value Decomposition (SVD), Principal Component Analysis (PCA) etc. are some of effective mathematical techniques (few others advance techniques e.g. tSNE,NMF,LIME,DeepLIFT,VAE etc.) are also used quite extensively in feature engineering(FE). Objective behind FE is to discover the concept and structure in a dataset, reduce dimensionality (basically reduce the number of independent variables and avoid curse of dimensionality) and redundancy, determine relevant set of base attributes, improve model generalization, training time etc. by analyzing data, variables, co-variance & correlation. SVD and PCA breaks down training data into several components that helps connect to the underlying concept through which we can reasonably establish the rationale of outcome. Like human, ML algorithm can also gracefully learn the concept if we present data with (a) adequate variability (more variation leads to more information) (b) minimal covariance (less similarities with other features leads to less redundancy thereby less noise) in a transformed vector space. Latent concept extraction become easier in such transformed dataset. We can draw better insight with less of data that helps explainability and also speeds up training of AI/ML models.
Build intuition: Before I dive deep into SVD and PCA, let’s build some intuition using an example from IMDb (Internet Movie DB) that helps discern hidden concept of relationship between users and movie’s types. We can extend the same mechanics to discern concepts between books and readers like amazon does, typical adv. clicks by type of users, matching financial products such as auto-loan, mortgage, investments or advisory products with users like some financial institutions does and so on.
Below is a small sample from movie rating database. Why a particular user has rated a movie that way, can we unravel hidden constituents that connects a user to a movie and justifies the rating?
SVD (Powerful matrix decomposition tool in linear algebra) helps us unravel such concepts or components that connects a user to any movie in a given observation dataset. Mathematically we can conceive Rating = fn(user interest , movie type); i.e. rating value is some function(unknown) of user interest and movie type , if these two matches then value is high else low !!! SVD helps to break data into pieces(matrices) that reflects the semantics as why a user is rating that score.

If we could break rating matrix (main input dataset) into logical matrices such as relationship between Users to underlying themes/interests (U), Movies to themes (M) and Importance of each theme (I), then we can establish some rationale as why some users like certain movies more than other. Users may be varying degree of interests across genres of movies, for example, I like action, drama and adventure more than romantic! Similarly, movies can have variation in themes or concepts in the storyline. E.g. “The Dark night” has crime, drama, adventurous elements more than love, romance. The amount of each theme varies and depends upon particular user frame of reference. Ok, model development requires strong domain knowledge!!!
SVD helps to break original matrix into such matrices that helps data scientists to dive into the concept and build rational for any outcome. So, let’s understand how does SVD work and I assume readers have good understanding of linear algebra, I hope to keep derivation and explanation simple: –
Matrix key characteristics: –
Envision the derivation in 2D or 3D that helps generalize the concept in hyper feature space (multi D)
- Multiple a vector using a matrix (exploit the property of rotation and stretching of any matrix)

 SVD derivation: –
SVD derivation: –
Let’s have n dimensional space having n axes (orthogonal) having n vectors (v1, v2…vn) to go through transformation through matrix (A) of size m(rows) and n(cols).
In multi-dimensional feature space, Matrix A rotates and stretches (+) or compresses (-) vector (v).
i.e. Av1= σ1u1, Av2= σ2u2, Av3=σ3u3……Avn= σnun ; where σi is stretching factor and ui’s are orthogonal unit vectors
Graphical Representation


Now we have obtained all components of matrix (A). I will run a python code to determine actual values U, V and Σ of the small dataset I showed above. This is very small dataset that I will be using for illustration (How to derive concept to establish rationale behind movie ratings): –
U,S,VT=svd(A)
S = [19.09 7. 2.35 1.25 0.88 0.62] This array lists out concepts strength in descending order.
Let’s take only top 3 relevant concepts from S (Sigma)as below and diagonalize that
Sigma =
array([[19.09, 0. , 0. ],
[ 0. , 7. , 0. ],
[ 0. , 0. , 2.35]])
We take three orthonormal columns from U and top 3 VT as below
U=[[-0.27 -0.1 -0.7 ]
[-0.4 -0.29 0.33]
[-0.38 -0.32 -0.33]
[-0.31 0.5 -0.08]
[-0.31 0.39 0.38]
[-0.37 -0.25 0.33]
[-0.45 -0.21 0.05]
[-0.31 0.55 -0.18]]
And VT =[[-0.41 -0.42 -0.48 -0.44 -0.35 -0.32]
[-0.33 -0.28 -0.02 -0.3 0.52 0.67]
[ 0.42 -0.01 -0.82 0.24 0.29 0.05]]
SVD simplifies the analysis of dataset (e.g. movies, book ratings etc.) by going through these three components. In the above example if one analyzes matrix U (User to concept), 1st user puts more emphasis on 3rd concept and movie “Bahubali” shows quite a significant score in 3rd concept, this means 1st user likes action and/or war movie quite a lot. Likewise, this technique helps deciphers connections between users and some latent factors (U matrix), strength of such latent factors ( ∑ matrix) and connection between movies and latent factors (VT matrix).
Summary: XAI is quite a crucial task for successful implementation of AI/ML model in any industry, whether its driverless vehicles, medical diagnosis, financial decision or legal system. XAI requires infusion of domain understanding, strong grip of linear algebra, statistics analysis, feature engineering, data preprocessing, visualization etc. Approach should be to start with small subset of unbiased dataset and cruise through involved mathematics to build the foundation to map numerical outcome to the business outcome. Several other feature engineering and dimensional reduction techniques such as PCA, NMF, tSNE, LDA etc. are quite in use these days by ML practitioners, each technique arrives the similar concept through different approaches. All of these and many more upcoming advance mathematical techniques by academicians are worth practicing upon to strengthen XAI capability. I hope to have brought some insight about XAI importance and approach while taking the help of SVD technique. Please stay tuned for more upcoming articles related to XAI.